2022年03月25日
リターンとリスクを適切に把握した資産運用について
特定の金融商品や資産クラスのリターンとリスクに関する情報は、金融商品情報を提供するウェブサイトや証券会社等から提供され、投資家が金融商品を選ぶ時の重要な情報の一つになっています。リターンとリスクは、過去の株価や投資信託の基準価格(以下、株価等)から算出されたもので、将来の株価等を表すものではありませんが、将来どのくらい利益が期待できるか、どれくらい損を覚悟すべきか考えるとき、利用している投資家は多いと思います。改めて、リターンとリスクの意味や性質を理解し、将来の資産額の把握に活用することで、資産運用の参考にして頂けたらと思います。
リターンに関する情報は、一定期間のトータルリターンや1年あたりの平均リターンの形で提供されています。例えば、3年のトータルリターンは、3年前の株価等を基準に算出時点の株価等の騰落率で、3年間の騰落率を直接表しています。1年あたりの平均リターンは、算出期間が6ケ月、3年、5年、10年等となっている時は、算出方法の一例として、算出期間に応じた起算日から算出日までの騰落率に1を加えた値を年数乗根した値になっています。複数年のトータルリターンは、1年あたりの平均リターンの累乗、つまり複利計算で算出できます。
1年あたりの平均リターン={1+(算出日株価-起算日株価)/起算日株価}^1/年数
リスクは、株価等の変動率の1年あたりの標準偏差(σ)が表示されています。株価等の変動率は、ランダムに動き、ほぼ正規分布になることが知られています。ある時点の株価等を基準に、1年後の株価等の変動率は、1年あたりの平均リターンを中心にほぼ正規分布することになります。正規分布では、平均値を中心に±1σの範囲に、約68%が入ります。つまり、平均値+1σよりも上になる確率は約16%で、平均値-1σより上になる確率は約84%になります。平均値より上になる確率は、50%です。株価等の変動率がランダムに分布する時、その標準偏差は、算出期間の平方根に比例して大きくなる性質があります。例えば、基準時点から3年後の株価等の変動率の標準偏差は、1年あたりの標準偏差の3の平方根倍(1.73倍)になります。1日の変動率データから算出した1日あたりの標準偏差がわかる場合、1年あたりの標準偏差は、1年の株式取引日数が252日として、1日あたりの標準偏差に252の平方根(15.8)を乗じた値になります。つまり、数年先の変動率の分布の標準偏差は、単純に1年の標準偏差を年数倍したものではなく、年数の平方根倍した値になる性質があります。
n年後の変動率の標準偏差=1年あたりの標準偏差×nの平方根
実際の金融商品の過去の株価等を用いてリターンとリスクを算出すると、算出期間や時期により変動していますので、確定的なことは何も言えませんが、将来のリターンとリスクも変動した値になると推定できます。しかし、単純化して将来の株価等を考えるため、仮にリターン6%/年、リスク(標準偏差σ)15%/年と一定の金融商品があるとすると、現在の株価等に対して1年後の株価等の変動率が、-9%から+21%の範囲に約68%の確率で入ることになります。言い換えると、-9%より高値になる確率は約84%、+6%より高値になる確率は50%、+21%より高値になる確率は約16%です。1年と言う短期で見ると、元本割れになる可能性が、ある程度残るイメージです。
出典 筆者作成(リターンとリスクの性質が同じ幾何ブラウン運動モデルで算出)
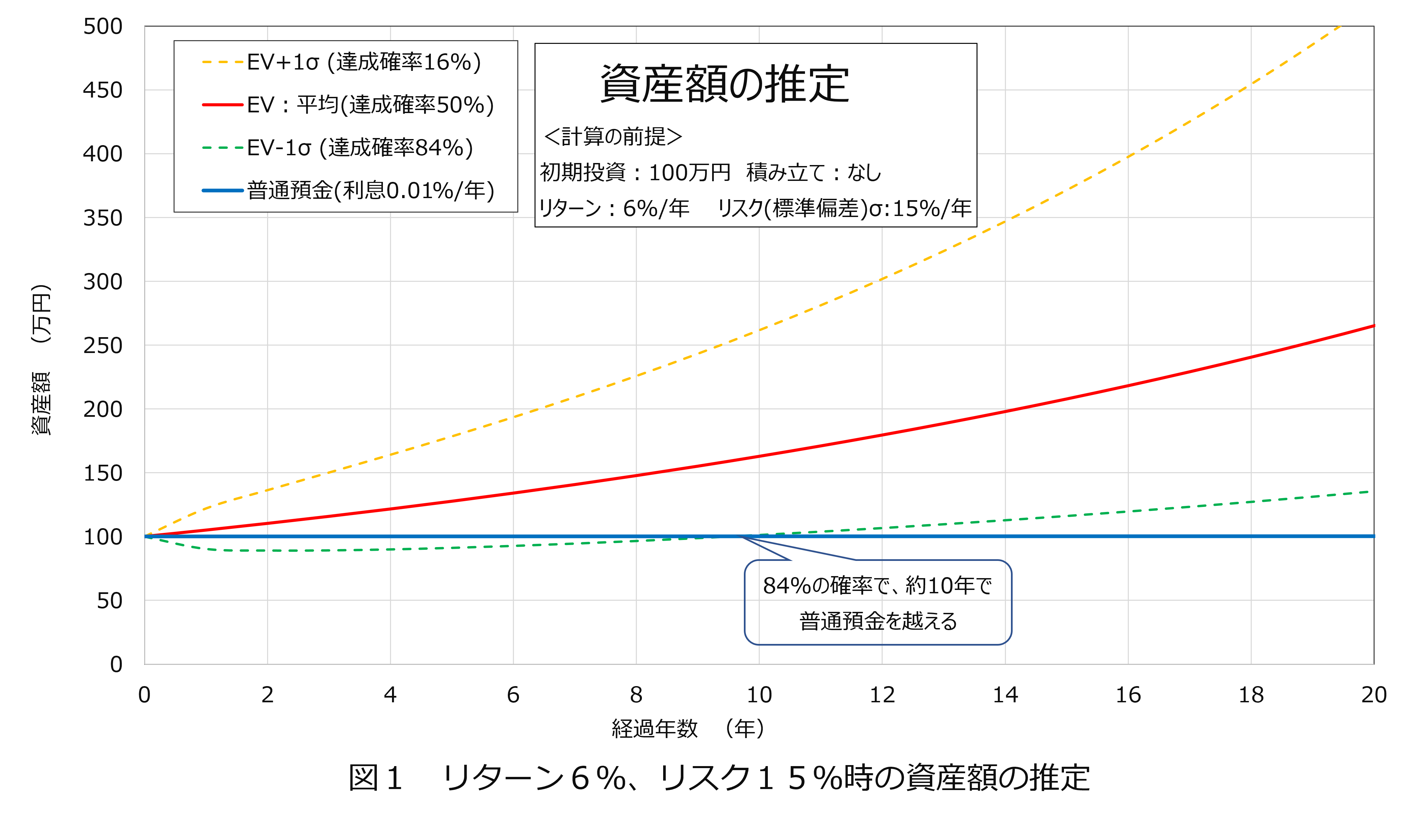
同じ金融商品を、同じリターンとリスクで、長期保有したらどうなるでしょうか。先に述べたリターンの性質の複利効果とリスクは期間の平方根に比例する性質を考慮して、元本100万円、積立なしの条件で資産額を推定したのが、図1です。約10年後に、元本に対する変動率が+0%より高値になる確率、つまり元本割れしない確率が、約84%になり、その後さらに元本割れの確率が下がることがわかります。リターン6%/年、リスク15%/年とリスクが高め金融商品でも、損失が出る確率が抑えられ、長期投資のメリットが出ます。
出典 筆者作成
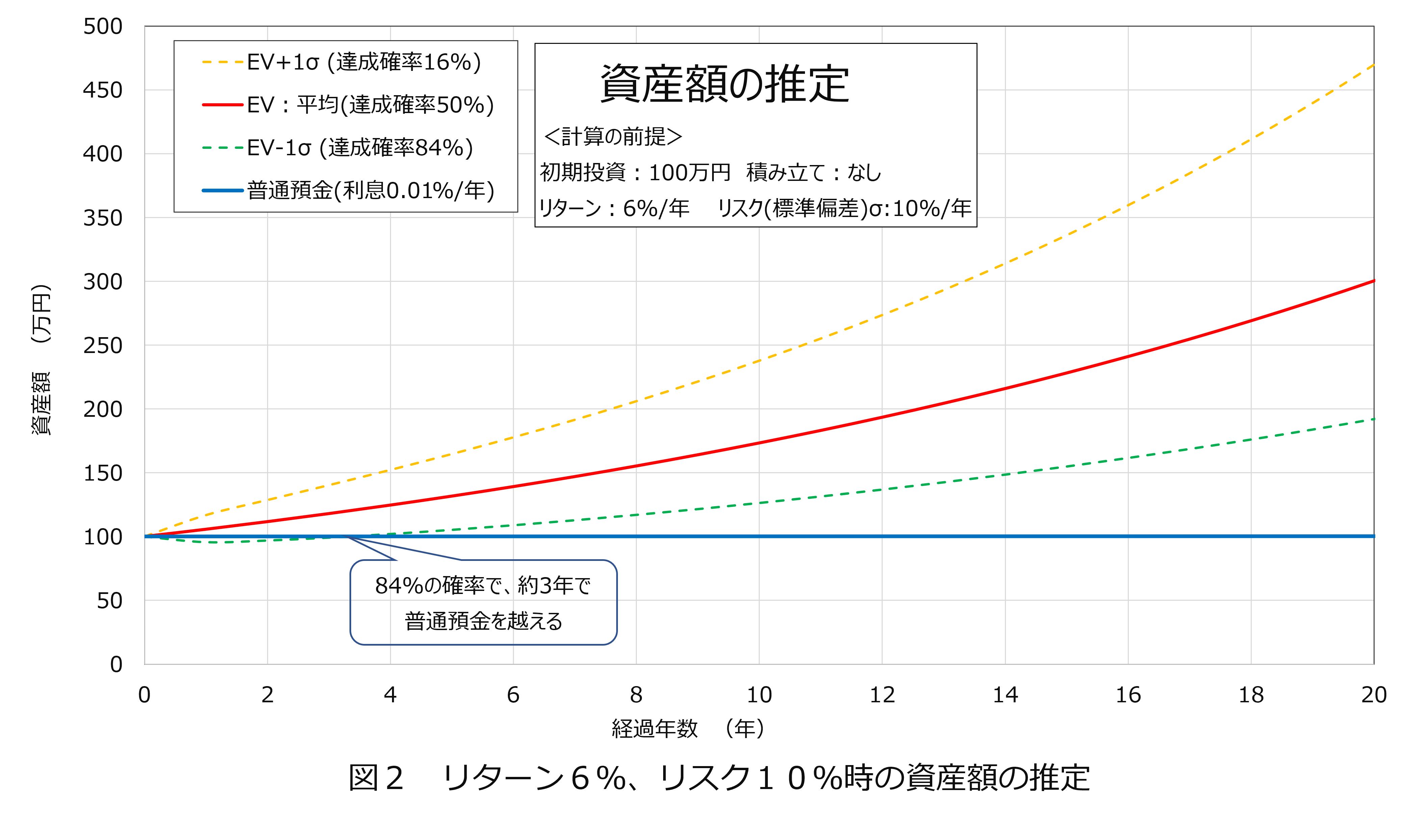
長期投資では、リターンの複利効果とリスクの期間の平方根に比例する性質により、リスク低減的な効果が得られますが、適切なアセットアロケーションによる分散投資でリスクを低減させた上で、長期投資することで相乗効果が得られます。適切なアセットアロケーションによる分散投資とは、お互いに値動きの相関性が低い資産クラスの金融商品を組み合わせて投資する方法です。例えば、米国株式、J-REIT、金は、それぞれ単体の金融商品としては、図1のようなリスクの高めの金融商品ですが、3つは比較的値動きの相関が低いため、組み合わせると、リターンはそのままで、リスクだけを下げて資産運用できる可能性があります。図2は、図1の時からリスクだけ15%/年から10%/年に下げて算出したものです。約3年後に、元本に対する変動率が+0%より高値になる確率が約84%になり、20年後には資産額が190万円(変動率+90%)以上になる確率が約84%になっています。分散投資の効果が確認できます。
過去情報に基づくリターンとリスクを数値として把握するだけでなく、把握した数値を活用して将来の資産額やその振れ幅の概算を推定することは、過度にリスクを取った投資や慎重過ぎる資金運用を是正し、投資家それぞれに合った長期の資産運用を行う上で役に立つと考えます。また、将来のライフプランに必要な資金は堅実に確保すべきものですが、資産運用である程度高い確率で期待できる金額がわかれば、それに充てることも検討できます。
西川 敏明 2022年03月25日